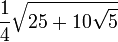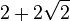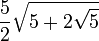Trong hình học Euclide,
đa giác đều là đa giác có tất cả các cạnh bằng nhau và các góc ở đỉnh bằng nhau.Đa giác đều được chia làm hai loại là: đa giác lồi đều và đa giác sao đều.
Tính chất tổng quát
Các tình chất này được áp dụng cho cả hình đa giác lồi đều và hình đa giác sao đều.
Tất cả các đỉnh của đa giác đều đều nằm trên một đường tròn. Chúng là các điểm đồng viên. Tất cả các đa giác đều đều có một đường tròn ngoại tiếp
Cũng với tính chất độ dài các cạnh của đa giác đều thì bằng nhau, kéo theo rằng tất cả các đa giác đều đều có các đường tròn nội tiếp.
Một đa giác đều
n cạnh có thể được dựng bằng compa và thước kẻ khi và chỉ khi các thừa số nguyên tố lẻ của
n khác số nguyên tố Fermat.
Tính đối xứng
Nhóm đối xứng của đa giác đều
n cạnh được gọi theo tên tiếng anh là nhóm
dihedral group Dn:
D2,
D3,
D4,... Nó bao gồm sự quay quanh tâm
Cn (tâm đối xứng), cùng với tính đối xứng của
n trục đi qua tâm này. Nếu
n là chẵn thì một nửa số trục đối xứng đi qua hai đỉnh đối nhau của đa giác và nửa còn lại đi qua trung điểm của hai cạnh đối. Nếu
n là lẻ thì tất cả các trục đới xứng đều đi qua một đỉnh và trung điểm của cạnh đối diện ới đỉnh ấy
Đa giác lồi đều
Tất các đa giác đơn đều (một đa giác đơn là một đa giác mà không tự cắt)là các đa giác lồi đều. Các đa giác mà có cùng số đo các cạnh thì đồng dạng.
Một đa giác lồi đều
n cạnh được chỉ rõ bởi công thức Schläfli của nó: {
n}.
- Đa giác đều 1 đỉnh: suy biến trong không gian bình thường {1}
- Nhị giác đều: một "đoạn thẳng đôi" - suy biến trong không gian bình thường {2}
- Tam giác đều {3}
- Hình vuông {4}
- Ngũ giác đều {5}
- Lục giác đều {6}
- Thất giác đều {7}
- Bát giác đều {8}
- Cửu giác đều {9}
- Thập giác đều {10}
Tam giác đều  Các cạnh của tam giác đều | Hình vuông | Ngũ giác đều  Cách vẽ hình ngũ giác đều |
| Lục giác đều | Thất giác đều |
|
Trong một số hoàn cảnh các đa giác đã được xét đến đều là các đa giác đều. Trong nhiều trường người ta thường bỏ chữ
đều đi. Ví dụ như mọi mặt của đa diện đều có thể là các hình đa giác đều như: tam giác đều, hình vuông, ngũ giác đều, etc.
Góc
Với một đa giác đều n đỉnh, đỉnh trong được tính bằng công thức:
 (hay bằng với
(hay bằng với  ) độ,
) độ,
hay

độ radian,
hay

tính theo vòng,
và với mỗi góc ngoài (kề bù với góc trong)được tính theo công thức

độ, với tổng của các góc ngoài bằng 360 độ hay 2π độ radian hay vòng quay.
Đường chéo
Với
n > 2 số đường chéo là
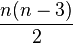
, i.e., 0, 2, 5, 9, ... Chúng chia đa giác thành 1, 4, 11, 24, ... phần.
Diện tích

Trung đoạn của lục giác đều
Diện tích A của đa giác lồi đều
n cạnh là:
theo độ
 ,
,
hay theo độ radian
 ,
,
với
t là độ dài của một cạnh.
Nếu biết bán kính, hay độ dài đoạn thẳng nối tâm với một đỉnh, diện tích là: tính theo độ

hay theo độ radian
 ,
,
với
r là độ lớn của bán kính
Đồng thời, diện tích cũng bằng nửa chu vi nhân với độ dài của trung đoạn,
a, (đoạn vuông góc hạ từ tâm của đa giác xuống một cạnh). Vì vây ta có
A =
a.n.t/2, với chu vi là
n.t, và ở dạng đơn giản hơn 1/2
p.a.
Với cạnh
t=1, ta có:
theo độ

hay theo độ radian (
n khác 2)

giá trị được viết trong bảng sau:
| Số cạnh | tên hình | Diện tích chính xác | Xấp Xỉ |
| 3 | tam giác đều |  | 0.433 |
| 4 | hình vuông | 1 | 1.000 |
| 5 | ngũ giác đều | 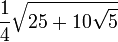 | 1.720 |
| 6 | lục giác đều |  | 2.598 |
| 7 | thất giác đều | | 3.634 |
| 8 | bát giác đều | 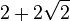 | 4.828 |
| 9 | cửu giác đều | | 6.182 |
| 10 | thập giác đều | 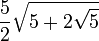 | 7.694 |
| 11 | đa giác đều 11 đỉnh | | 9.366 |
| 12 | đa giác đều 12 đỉnh |  | 11.196 |
| 13 | đa giác đều 13 đỉnh | | 13.186 |
| 14 | đa giác đều 14 đỉnh | | 15.335 |
| 15 | đa giác đều 15 đỉnh | | 17.642 |
| 16 | đa giác đều 16 đỉnh | | 20.109 |
| 17 | đa giác đều 17 đỉnh | | 22.735 |
| 18 | đa giác đều 18 đỉnh | | 25.521 |
| 19 | đa giác đều 19 đỉnh | | 28.465 |
| 20 | đa giác đều 20 đỉnh | | 31.569 |
| 100 | đa giác đều 100 đỉnh | | 795.513 |
| 1000 | đa giác đều 1000 đỉnh | | 79577.210 |
| 10000 | đa giác đều 10000 đỉnh | | 7957746.893 |
The amounts that the areas are less than those of circles with the same perimeter, are (rounded) equal to 0.26, for n<8 a little more (the amounts decrease with increasing
n to the limit π/12).





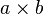






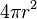 , hoặc
, hoặc 

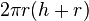
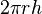








 (hay bằng với
(hay bằng với  ) độ,
) độ, độ radian,
độ radian, tính theo vòng,
tính theo vòng, độ, với tổng của các góc ngoài bằng 360 độ hay 2π độ radian hay vòng quay.
độ, với tổng của các góc ngoài bằng 360 độ hay 2π độ radian hay vòng quay.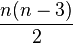 , i.e., 0, 2, 5, 9, ... Chúng chia đa giác thành 1, 4, 11, 24, ... phần.
, i.e., 0, 2, 5, 9, ... Chúng chia đa giác thành 1, 4, 11, 24, ... phần.
 ,
, ,
,
 ,
,